盘子|圆盘_递归与分治策略第一节：递归和典型递归问题

篇首语：本文由编程笔记#小编为大家整理，主要介绍了递归与分治策略-第一节：递归和典型递归问题相关的知识，希望对你有一定的参考价值。

文章目录

• 一&＃xff1a;LeetCode中有关递归和分治的题目
• 二&＃xff1a;递归与分治概述
• 三&＃xff1a;递归基本概念
• 四&＃xff1a;典型递归问题分析
• • &＃xff08;1&＃xff09;阶乘
  • &＃xff08;2&＃xff09;Fibonacci数列
  • &＃xff08;3&＃xff09;排列问题
  • &＃xff08;4&＃xff09;整数划分
  • &＃xff08;5&＃xff09;汉诺塔
  
  
• 五&＃xff1a;递归算法原理
• 六&＃xff1a;递归算法优缺点

递归题目&＃xff1a;链接

分治题目&＃xff1a;链接

递归与分治&＃xff1a;任何可以用计算机求解的问题所需要的计算时间都和其规模有关&＃xff0c;如果问题的规模越小&＃xff0c;解题所需的计算时间往往也越短&＃xff0c;从而也比较容易处理&＃xff0c;例如

• 对于$n$个元素的排序问题&＃xff1a;当$n\&＃61;1$时不需要任何计算&＃xff1b;当$n\&＃61;2$时&＃xff0c;只需要做一次比较即可排好序&＃xff1b;当$n\&＃61;3$时则两次。而当$n$较大时&＃xff0c;这个问题就不好处理了

所以要想直接解决一个较大的问题&＃xff0c;有时是相当有困难的。所以分治法的设计思想是&＃xff1a;将一个难以直接解决的大问题分割成一些规模较小的相同问题&＃xff0c;以便各个击破&＃xff0c;也即分而治之。如果原问题可以分割为$k$个子问题&＃xff0c;$1<k\le n$&＃xff0c;且这些子问题都可解&＃xff0c;并可利用这些子问题的解求出原问题的解&＃xff0c;那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式&＃xff0c;这为使用递归技术提供了方便。在这种情况下&＃xff0c;反复应用分治手段&＃xff0c;可以使子问题于原问题类型一致而其规模不断缩小&＃xff0c;最终使子问题缩小到容易求出其解&＃xff0c;由此自然引出递归算法。分治与递归像一对孪生兄弟&＃xff0c;经常同时应用在算法设计中&＃xff0c;并由此产生许多高效算法

递归&＃xff1a;递归算法是指直接或间接调用自身的算法&＃xff1b;递归函数是指用函数自身给出定义的函数。在计算机算法设计与分析中&＃xff0c;递归技术非常有用。使用递归技术往往可以使函数的定义和算法的描述简洁且易于理解&＃xff0c;而且有些数据结构&＃xff08;例如二叉树&＃xff09;由于其本身具有递归特性&＃xff0c;所以也特别使用递归的形式来求解

构造递归算法的基本步骤为

• 确定递归边界
• 描述递归关系
• 构造递归函数

&＃xff08;1&＃xff09;阶乘

阶乘&＃xff1a;$n!\&＃61;n\times (n-1)\times ...\times 1$&＃xff0c;可递归定义如下

• 第一个式子是递归边界&＃xff0c;如果没有边界就有可能会引发无穷递归
• 第二个式子是用较小自变量的函数来表示较大自变量的函数值&＃xff0c;相当于问题规模减小
  

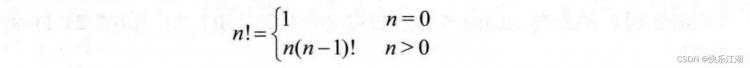
这个问题很简单&＃xff0c;递归定义式很容易给出&＃xff0c;所以编写代码如下

public class Factorial
public static int factorial_recurse(int n )
if(n &＃61;&＃61; 1)return 1;
return n * factorial_recurse(n-1);

public static void main(String[] args)
Scanner scanner &＃61; new Scanner(System.in);
while(scanner.hasNextInt())
int n &＃61; scanner.nextInt();
System.out.println(n&＃43;"!等于&＃xff1a;" &＃43; factorial_recurse(n));





当然&＃xff0c;递归解法也有其对应的非递归解法

public class Factorial
public static int factorial_none_recurse(int n)
int ret &＃61; 1;
for(int i &＃61; 1; i <&＃61; n; i&＃43;&＃43;)
ret *&＃61; i;

return ret;

public static void main(String[] args)
Scanner scanner &＃61; new Scanner(System.in);
while(scanner.hasNextInt())
int n &＃61; scanner.nextInt();
System.out.println(n&＃43;"!等于&＃xff1a;" &＃43; factorial_none_recurse(n));





&＃xff08;2&＃xff09;Fibonacci数列

Fibonacci数列 &＃xff1a;无穷数列【1 1 2 3 5 8 13 21 34 55…】称为Fibonacci数列&＃xff0c;在Fibonacci数列中从第三个数字开始&＃xff0c;每一个数字都是前两个数字之和&＃xff0c;这是一个典型的递归问题&＃xff0c;其递归定义式如下

很明显这个问题需要两个递归边界

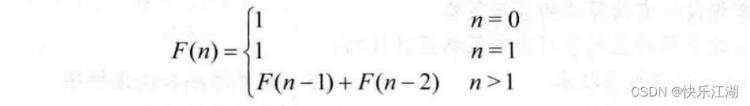
问题还是比较简单&＃xff0c;所以编写代码如下

public class Fibonacci
public static int fibonacci_recurse(int n)
if(n <&＃61; 1)return 1;
return fibonacci_recurse(n-1) &＃43; fibonacci_recurse(n-2);

public static void main(String[] args)
Scanner scanner &＃61; new Scanner(System.in);
while(scanner.hasNextInt())
int n &＃61; scanner.nextInt();
System.out.println("第" &＃43; n&＃43;"个fibonacci数为&＃xff1a;" &＃43; fibonacci_recurse(n));





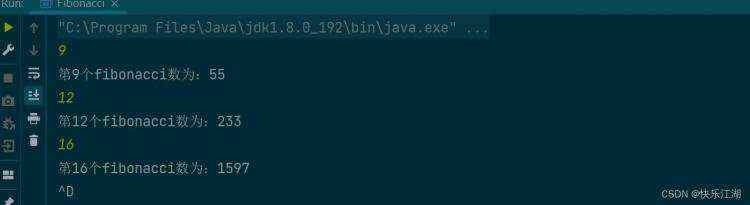
fibonacci数列的纯递归写法有很多的重复子问题&＃xff0c;所以其时间复杂度极高。所以对于其递归写法&＃xff0c;我们可以进行一定优化&＃xff0c;引入一个“备忘录”去解决这一部分重复子问题

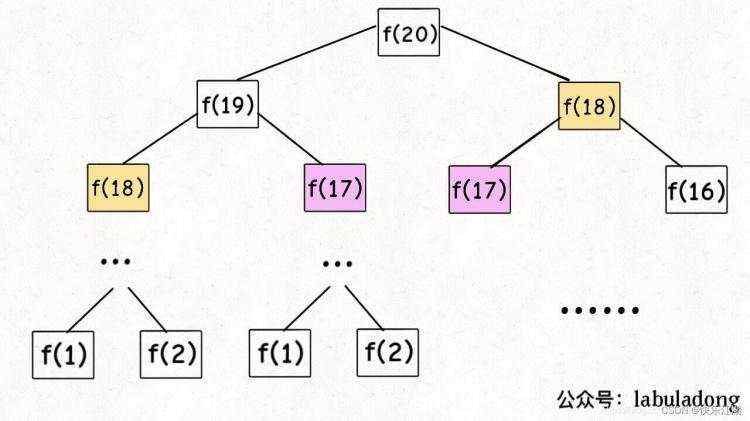
public class Fibonacci
public static int fibonacci_recurse(int n)
if(n <&＃61; 1)return 1;
return fibonacci_recurse(n-1) &＃43; fibonacci_recurse(n-2);

public static int fibonacci_recurse_optimize(int[] memo, int n)
if(n <&＃61; 1)return 1;
if(memo[n] !&＃61; 0)return memo[n];//如果备忘录有这个元素那就不用递归了
memo[n] &＃61; fibonacci_recurse(n-1) &＃43; fibonacci_recurse(n-2);//保存下来
return memo[n];

public static void main(String[] args)
Scanner scanner &＃61; new Scanner(System.in);
while(scanner.hasNextInt())
int n &＃61; scanner.nextInt();
int[] memo &＃61; new int[n&＃43;1];//备忘录&＃xff0c;元素如果为0表示没有被记录
long recurse_start_time &＃61; System.nanoTime();
System.out.println("(递归)第" &＃43; n&＃43;"个fibonacci数为&＃xff1a;" &＃43; fibonacci_recurse_optimize(memo, n));
long recurse_end_time &＃61; System.nanoTime();
long none_recurse_start_time &＃61; System.nanoTime();
System.out.println("(非递归)第" &＃43; n&＃43;"个fibonacci数为&＃xff1a;" &＃43; fibonacci_recurse_optimize(memo, n));
long none_recurse_end_time &＃61; System.nanoTime();
System.out.println("递归用时&＃xff1a;" &＃43; (recurse_end_time - recurse_start_time));
System.out.println("非递归用时&＃xff1a;" &＃43; (none_recurse_end_time - none_recurse_start_time));
System.out.println("----------------------------------------------------");

scanner.close();




&＃xff08;3&＃xff09;排列问题

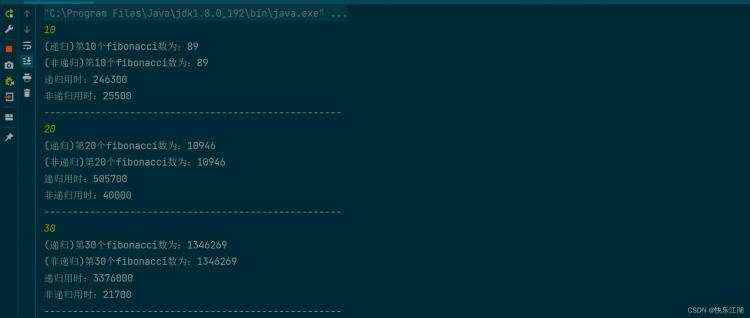
排列问题&＃xff1a;设计一个递归算法生成$n$个元素的全排列

采用递归解法&＃xff0c;可以将规模为$n$的全排列问题转换为规模为$n-1$的全排列问题。所以他可以看作是固定$[0,k]$位&＃xff0c;对$[k\&＃43;1,n]$位进行全排列&＃xff0c;当$k\&＃43;1\&＃61;n$时&＃xff0c;递归结束

如下为决策树&＃xff0c;每一个子决策树都是一个全排列问题&＃xff0c;

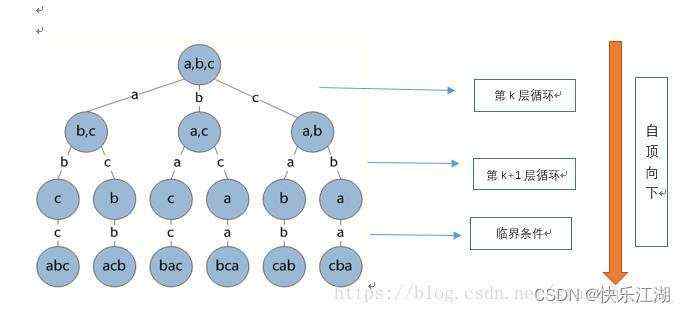
代码如下

public class Permutations
public static void swap(int[] test, int k, int i)
int temp &＃61; test[k];
test[k] &＃61; test[i];
test[i] &＃61; temp;

public static void perm(int[] list, int k, int m)
//只有一个元素&＃xff0c;递归结束&＃xff0c;这一种排列情况可以输出了
if(k &＃61;&＃61; m)
for(int i &＃61; 0; i <&＃61; m; i&＃43;&＃43;)
System.out.print(list[i]);

System.out.println();

//否则开始递归
else
for(int i &＃61; k; i <&＃61; m; i&＃43;&＃43;)
swap(list, k, i);
perm(list, k&＃43;1, m);
swap(list, k, i);



public static void main(String[] args)
int[] test &＃61; new int[]2, 3, 5, 7;
perm(test, 0, 3);




&＃xff08;4&＃xff09;整数划分

整数划分&＃xff1a;将正整数$n$表示成一系列整数之和&＃xff0c;即




n


&＃61;



n


1



&＃43;



n


2



&＃43;


.


.


.


&＃43;



n


k




n&＃61;n_1&＃43;n_2&＃43;...&＃43;n_k


n&＃61;n1​&＃43;n2​&＃43;...&＃43;nk​

在这里&＃xff0c;正整数$n$的这种表示称为正整数$n$的划分。正整数$n$的不同划分个数称为正整数$n$的划分数&＃xff0c;记为$p(n)$&＃xff0c;例如6有如下11种不同的划分方法&＃xff0c;所以$p(6)\&＃61;11$

6
5&＃43;1
4&＃43;2, 4&＃43;1&＃43;1
3&＃43;3, 3&＃43;2&＃43;1, 3&＃43;1&＃43;1&＃43;1
2&＃43;2&＃43;2, 2&＃43;2&＃43;1&＃43;1, 2&＃43;1&＃43;1&＃43;1&＃43;1
1&＃43;1&＃43;1&＃43;1&＃43;1&＃43;1


在正整数$n$的所有划分中&＃xff0c;用$q(n,m)$表示最大加数





n


1




n_1


n1​不大于$m$的划分个数&＃xff0c;正整数$n$的划分数$p(n)\&＃61;q(n,n)$

• 当$n\ge 1$时&＃xff0c;$q(n,1)\&＃61;1$&＃xff0c;因为当最大加数最大为1时&＃xff0c;任何正整数只有一种划分形式&＃xff0c;也即全1
• 由于最大加数不可能大于$n$&＃xff0c;所以当$m\ge n$时&＃xff0c;$q(n,m)\&＃61;q(n,n)$,$q(1,m)\&＃61;1$
• 正整数$n$的划分由
  
  
  
  
  
  n
  
  
  1
  
  
  
  &＃61;
  
  
  n
  
  
  
  n_1&＃61;n
  
  
  n1​&＃61; var cpro_id = "u6885494";